带淘汰制的自适应联盟竞赛算法

　　摘  要： 提出一种带的方法。实验结果表明，改进后的算法在计算效果上有一定程度的提高，同时解决了参数设置问题。

　　关键词： ；；；自适应参数调整；淘汰制

　　联盟竞赛算法LCA[1]（League Championship Algorithm）是一种基于迭代的群体智能优化算法。

　　参考文献[1]中的实验结果表明，联盟竞赛算法相比粒子群优化算法，计算效果和效率都有一定的优势，因此该算法具有较好的应用前景。目前国内外对该算法做的研究主要集中在算法的扩展上，参考文献[2]和参考文献[3]都是将算法扩展为能够解决约束优化问题的算法，参考文献[4]将算法扩展为解决组合优化问题的算法。

　　通过初步分析和实验证明，算法主要存在两个缺点：（1）需手动设置多个参数，且在算法的运行中参数是静态不变的，因此对每个优化问题，需尝试不同的参数组合分别运行算法以找到一个较好的结果；（2）算法鲁棒性较低，在优化不同函数时，全局搜索能力差距较大，大大降低算法的实用性。目前还没有文献解决这些问题。

　　针对以上两个缺点，本文提出一种带淘汰制的自适应联盟竞赛算法ALCAKS（Adaptive League Championship Algorithm with Knockout System）。

　　1 联盟竞赛算法

　　1.1 联盟竞赛算法基本流程

　　（1）初始化团队数量、阵型、比赛轮数S等，令当前迭代次数t=0；

　　（2）产生一个赛季的比赛赛程；

　　（3）将最优适应值的团队阵型保存到Xt；

　　（4）根据第t轮的比赛赛程进行比赛，并按照一定规则判断比赛输赢；

　　（5）t=t+1，若t>S，执行步骤（9）；

　　（6）更新团队阵型：每个团队产生一个新阵型，若新阵型适应值比当前阵型适应值更优，则替换当前阵型；

　　（7）判断是否要产生新赛程，若是则根据某种规则产生新赛程并替换旧赛程，否则继续使用旧赛程；

　　（8）转步骤（3）；

　　（9）输出全局最优解Xs。

　　

　　

　　    综上所述，算法要求手动设置pc、c1和c2三个参数，其在运行中是静态不变的。对每个优化问题，需设置不同的参数组合分别运行算法以找到一个较好的结果。此外，本文通过实验（实验结果见2.2节）发现算法鲁棒性较低。针对这些问题，本文提出一种带淘汰制的自适应参数调整方法。

　　2 带淘汰制的自适应联盟竞赛算法

　　    为下文提出自适应参数调整方法和引入淘汰制提供基础，本文先给出一种检测收敛过慢和陷入局部极值的方法。

　　2.1 检测收敛速度

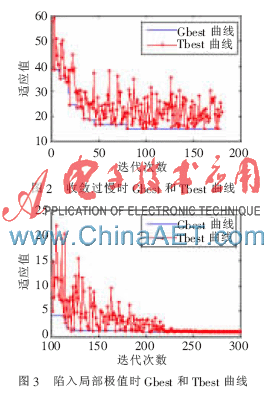
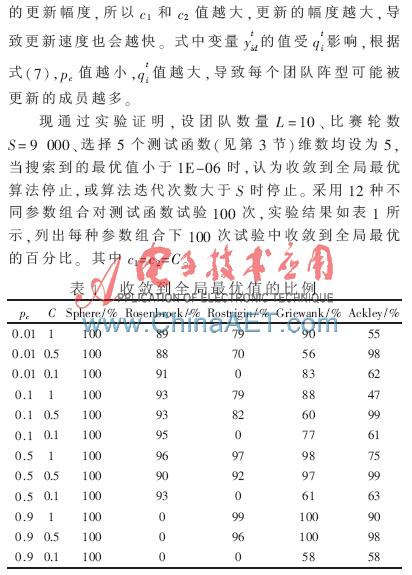
　　     为检测收敛速度，在算法中增加变量数组Gbest，Gbest[i]保存算法迭代到第i轮时的最好适应值。对于求解函数最小值时，任意i（0≤i≤S-2）都满足Gbest[i+1]≤Gbest[i]。当算法在第i轮（i≥w）出现|Gbest[i]-Gbest[i-w]|小于某阈值时，认为算法收敛过慢或陷入局部极值，其中w是窗口大小。为区分收敛过慢与陷入局部极值，再增加一个变量数组Tbest，Tbest[i]保存算法在第i轮中产生的新团队阵型中的最好适应值。如图2和图3所示，给出算法在优化Rosenbrock函数时出现的收敛过慢及陷入局部极值这两种结果，每种结果随着比赛轮数i的增加，Gbest[i]和Tbest[i]的变化曲线。

　　    在正常收敛速度下Gbest曲线稳步下降，Tbest曲线波动较大；从图2看出，当算法收敛过慢时，如在第80轮~180轮迭代期间，Gbest曲线无变化，但Tbest曲线波动较大；从图3看出，当算法陷入局部极值时，Gbest曲线和Tbest曲线变化幅度都较小，两条曲线最终重叠一起。

　　

　　

　　

　　根据上述的实验结果和分析得出：

　　（1）固定pc值，c1和c2值越大，收敛速度越快。当c1和c2值过小时，会导致收敛过慢而最终无法找到全局最优值。

　　（2）固定c1和c2值，pc值越小，收敛速度越快，全局寻优能力会稍微变弱。

　　根据以上观点，本文提出自适应参数调整方案如下：大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!

　　（1）算法初始时，设置较大参数值，较大pc值使算法专注于全局搜索，保持团队阵型多样性，较大c1、c2值使算法收敛速度不易过慢（本文实验设pc=0.8，c1=c2=1）；

　　（2）当算法收敛过慢时，减小pc以加快收敛速度；当算法陷入局部极值时，减小c1和c2值以减慢收敛速度，保持团队阵型多样性（本文实验pc=pc×0.8、c1=c1×0.8和c2=c2×0.8）。

　　2.3 淘汰机制

　　由表1可见，算法设置同一种参数组合时，针对不同优化问题，算法收敛到全局最优的比例差别较大，如当pc为0.01，c1和c2为1时，优化Ackley时收敛到全局最优的比例仅55%，而其他函数收敛到全局最优的比例都较高；当算法优化同一函数时，设置不同的参数组合收敛到全局最优的比例差距也较大，如当优化Ackley时，收敛到全局最优的比例最高有99%，最低仅47%。由此可见算法的鲁棒性较低。

　　为提高算法的计算效果，本文将淘汰机制引入算法。在体育团队联赛中一般有淘汰机制，如从32强到16强，这个过程必须淘汰一半的团队。本文借鉴淘汰赛思想提出淘汰策略：将所有团队按照团队适应值从优到差进行排序，选择排在前面的一半团队进行重新随机初始化。

　　首先算法陷入局部极值很可能是由最优适应值的团队已经陷入局部极值，且较差适应值的团队向较优适应值团队靠拢导致，所以只有将较优适应值团队淘汰后才能更好地跳出局部极值；其次为了保持参赛团队总数不变，直接对要淘汰的团队进行初始化，可解释为加入新团队参与比赛。

　　如果算法每轮迭代都使用该策略，将导致算法收敛过慢或无法收敛。因此本文提出基于收敛速度的淘汰机制：

　　（1）初始化开关变量Kswitch=false，值为true表示淘汰状态开启，该状态下算法每完成一个赛季都会执行淘汰策略；值为false表示淘汰状态关闭，不执行淘汰策略；

　　（2）当发现算法陷入局部极值时，令Kswitch=true；当发现算法收敛过慢时，令Kswitch=false；

　　2.4 带淘汰制的自适应联盟竞赛算法流程

　　综上所述，改进的联盟竞赛算法具体步骤如下：

　　（1）初始化团队数量、阵型、最大比赛轮数S、窗口大小w、Gbest、Tbest、阈值λs等；Kswitch=false、t=0；

　　（2）产生一个赛季的比赛赛程；

　　（3）将最优适应值的团队阵型保存到Xt；

　　（4）根据第t轮的赛程进行比赛，并判断比赛输赢；

　　（5）t=t+1，若t>S，执行步骤（11）；

　　（6）更新团队阵型和Gbest、Tbest；

　　（7）按式（8）检测算法是否收敛过慢或陷入局部极值；若算法收敛过慢，则按2.2节方案减小Pc值并令Kswitch=false；若算法陷入局部极值，则按2.2节方案减小C1和C2值并令Kswitch=true；大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!

　　 （8）若Kswitch=true，调用2.3节的淘汰策略；

　　 （9）判断是否要产生新赛程，若是则根据某种规则产生新赛程并替换旧赛程，否则继续使用旧赛程；

　　 （10）转步骤（3）；

　　 （11）输出全局最优解Xs。大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!

　　3 实验

　　本文通过5个经典的函数优化问题来测试改进后的联盟竞赛算法和原始联盟竞赛算法的性能。测试函数包括：Sphere、Rosenbrock、Rostrigin、Griewank和Ackley，其自变量取值范围分别为：[-100，100]、[-2.048，2.048]、 [-5.12，5.12]、[-32.76，32.76]、[-5.12，5.12]。

　　实验采用随机初始化团队阵型，函数值作为适应值，结束条件为最大迭代次数，由于5个测试函数的全局最优值都是0，假设最优值<λs时，认为算法收敛到全局最优。设团队数量L=10、迭代次数S=2 000、函数维数n=5、λs=1E-06，w=40，对LCA采用12种不同参数组合。

　　将ALCAKS和LCA的不同参数组合对每个测试函数分别试验100次。实验结果如表2和表3所示，对LCA只列出效果较好的3种参数组合。表2列出算法对每个测试函数在100次实验中收敛到全局最优的比例。表3列出算法对测试函数在100次实验中收敛到全局最优的最优值平均值。

　　

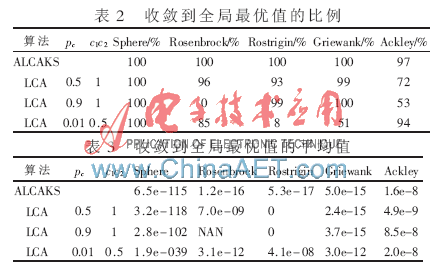
　　从表2、表3可以看出相比LCA算法，本文ALCAKS算法鲁棒性和全局搜索能力有一定程度的提高，因此本文提出的改进方案是可行的。

　　参考文献

　　[1] KASHAN A H. League championship algorithm： a new algorithm for numerical function optimization [C]. International Conference of Soft Computing and Pattern Recognition， 2009.

　　[2] KASHAN A H. A new algorithm for constrained optimization inspired by the sport league championships [C].  Evolutionary Computation（CEC）， 2010.

　　[3] KASHAN A H. An efficient algorithm for constrained global optimization and application to mechanical engineering design： League championship algorithm（LCA）[J]. Computer-Aided Design， 2011， 43： 1769-1792.

　　[4] POURALI Z， AMINNAYERI M. A novel discrete league championship algorithm for minimizing earliness/tardiness penalties with distinct due dates and batch delivery consideration[C]. Advanced Intelligent Computing， 2012.

　　[5] KASHAN A H， KARIMI B， JOLAI F. Effective hybrid genetic algorithm for minimizing makespan on a single-batch-processing machine with non-identical job sizes [C]. Int J Prod Res， 2006.